Introduction
In this experiment we will determine the rate constant of the diffusion-controlled quenching of photoexcited anthracene by CBr4. n-hexane is used as a solvent.
When anthracene is exposed to UV/visible light (photons) it will go into a photoexcited state:
(R1)

Photoexcited anthracene will convert back to its ground state during approximately 5×10-9s by emitting photons of less energy than the exciting photons, i.e., anthracene shows fluorescence.
The energy of the (exciting) photons is given by the relationship: (1)
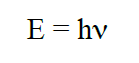
where h is Planck’s constant (h = 6.6256 ×10-34J s) and ν is the frequency of the photon. The frequency ν is coupled to the wavelength λ through the speed of light c (c = 299 792 458 m s-1) by the relationship: (2)
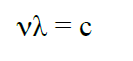
Carbontetrabromide (CBr4) can effectively remove (“quench”) the excess energy of photoexcited anthracen without the emission of a photon. The energy transferred to CBr4 is converted into heat in a process known as thermal conversion. This describes the quenching of anthracene’s photoexcited state by CBr4.
The reaction between CBr4 and photoexcited anthracene is so fast that each time CBr4 and photoexcited anthracene come close to each other, i.e., within a certain “reaction distance”, the reaction (quenching) happens immediately.
Schematically the quenching process of anthracene by CBr4 can be described as follows: (A = photoexcited anthracene, B = CBr4, P = product, that is anthracene in the ground state, and CBr4)(R2)
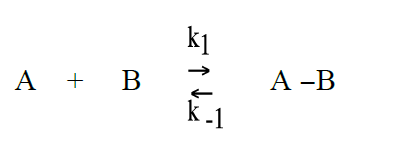
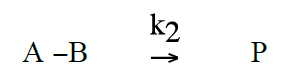
The reaction rate for the formation of P is given by:
(3)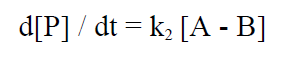
Since P forms very quickly we can assume that the A-B complex is in a steady state, i.e.
(4)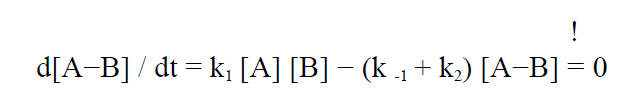
where the steady state concentration of A-B is given by:
(5)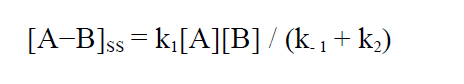
The reaction rate v for the steady state assumption becomes:
(6)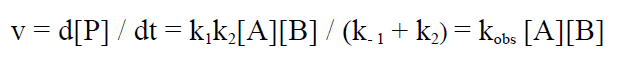
with kobs given as
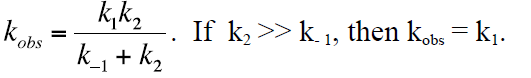
Diffusion controlled mass transport
In a diffusion controlled reaction the transport of molecules through diffusion is rate determining, hence the name diffusion controlled reactions. If the reaction rate is exactly the same as the diffusion rate the situation is called full microscopic diffusion control. In macroscopic diffusion control the reaction rate depends on how fast the solutions containing the reactants are mixed together. This is also called mixed control.
Describing the process of a full diffusion controlled reaction we start out with Fick's first law:
(7)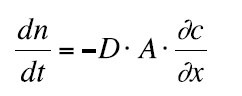
Equation 7 describes diffusion (change of number of moles n of a substance with time) along the x–axis. D is the diffusion coefficient and A is the surface area for which the diffusing molecules pass through.
Lets assume that we have a solution of uncharged molecules A and B with molecular radii of rA and rB respectively and that they react with each other. Molecule A is at rest and molecule B diffuses towards A:
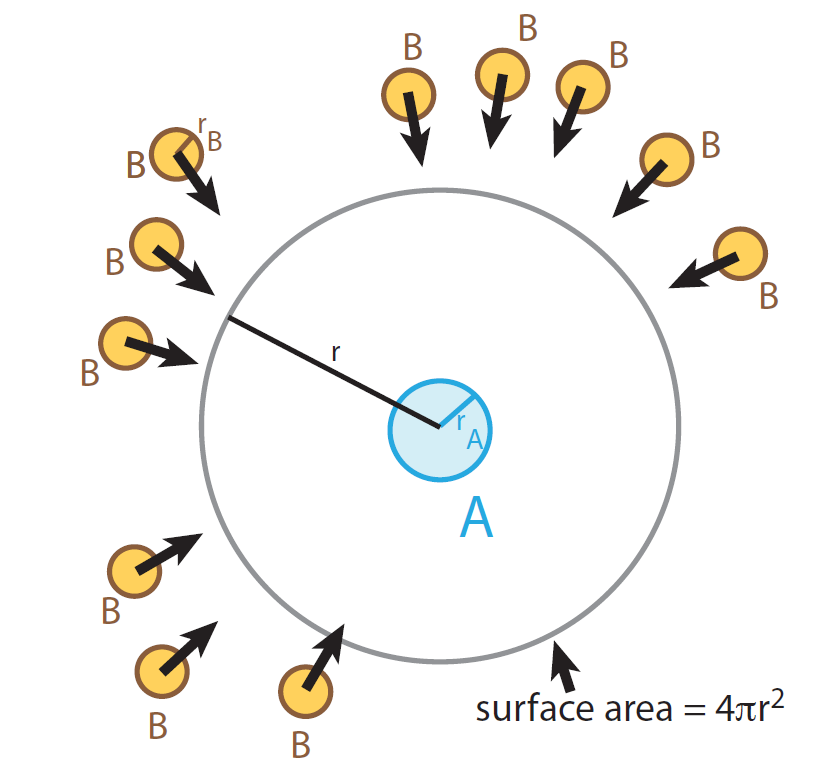
The diffusion rate dnB / dt = v diff, B through the surface of the sphere 4π r2 is given by Fick's first law:
(8)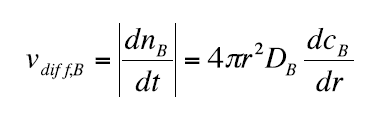
Separation of the variables gives:
(9)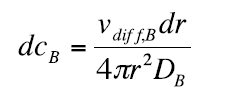
Integration of equation 9 gives:
(10)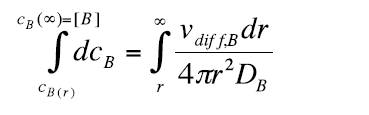
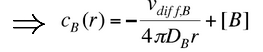
We have assumed that molecule A is not moving. If molecule A is diffusing, we get:
(12)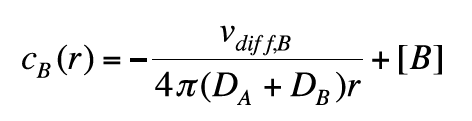
In full microscopic diffusion control a molecule B will react immediately as soon as a critical distance dAB is reached. For r ≤ dAB we have cB = 0, which leads to the condition:
(13)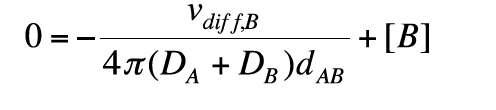
which can be rearranged to
(14)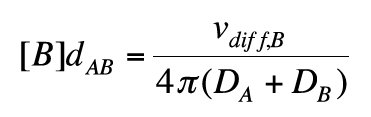
By combining Eq. 14 with Eq. 12, we can write:
(15)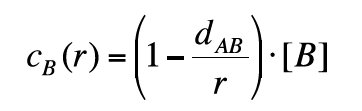
Equation 13 gives the following expression for vdiff, B:
(16)

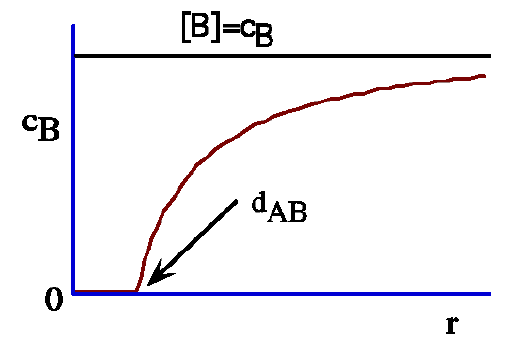
The diffusion rate of the B molecules towards a molecule A,
resulting in a chemical reaction when B molecules reach
the critical distance dAB.
The reaction rate when all A molecules are taken into account becomes:
(17)
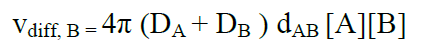
where the rate constant for a full diffusion controlled process is:
(18)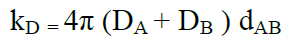
Expressing the diffusion coefficient D according to the Stokes-Einstein equation:
(19)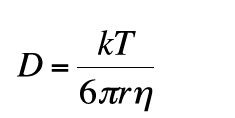
(k = Boltzman constant, T = temperature, η = viscosity, r= radius of spherical molecule) gives:
(20)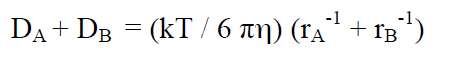
If dAB = rA + rB , kD can be written as:
(21)
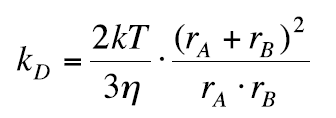
when rA = rB, kD can be written as:
(22a)
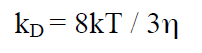
Equation 22a relates to a single molecule. For NA molecules (1 mol) we get:
(22b)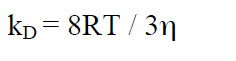
The viscosity η of water at 25 °C is 0.8904 cP (1P (Poise) = 1 g / cm s). Show that at 25°C, kD = 7.4 × 109 M-1 s-1 which defines an upper limit for non-ionic reactants. Equation 22 is often called the Stokes-Einstein-Smoluchowski (SES) equation.
Fluorescence quenching
The reaction we are studying in this experiment happens between an electronic excited anthracene molecule (named A*) and a quencher, CBr4 (named Q):
(R4)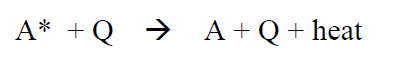
Q quenches excitations (thereby the name). In the quenching process the excited state in A (A*) is transferred by Q through a “charge-transfer-complex” composed of A* and Q (A+ - Q-), which then decomposes into ground state A and Q:
(R5)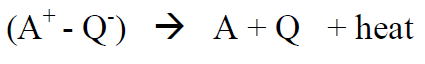
For CBr4 as quencher, the excess energy of excited anthracene is transferred from anthracene to CBr4.
The following elementary reactions can be considered during the excitation and quenching process:
(R6)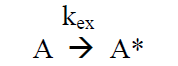
(R7)
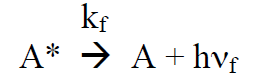
(R8)
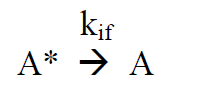
(R9)
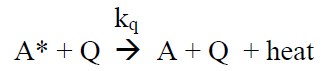
Under continuous irradiation, A* is in a steady state defined by the reactions R6 – R9:
(23)
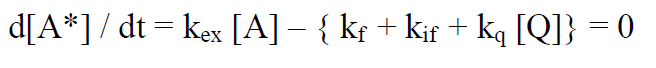
the steady state concentration [A*]ss :
(24)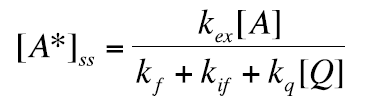
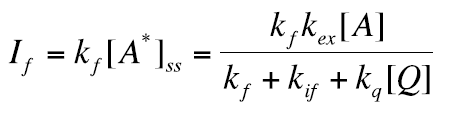
Relaxation time of A*
The relaxation time (lifetime) τ is defined as the time a variable (for example a concentration) has decreased exponentially to 1/e of its original value.In the absence of Q, A* decays by processes R7 and R8, and the relaxation of A* into the ground state A in darkness is given by
(26)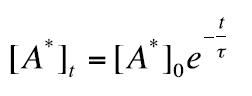
Were the fluorescence lifetime (relaxation time) τ is given as: τ = 1 / (kf + kif)
The Stern-Volmer plot
The intensity If of the fluorescent emission intensity is given by eq. 25. In the absence of quencher Q, the intensity is I0=kf kex[A]/kf+kif ,while in the presence of Q If is given by eq. 25. Calculating the ratio I0 / If we get
(27)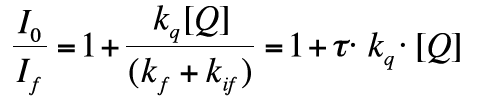
because τ is given as 1 / (kf + kif).
Plotting (I0 / I) -1 versus [Q] results in a straight line with slope + kqτ. Knowing the relaxation time τ of photoexcited anthracene we can determine the diffusion controlled rate constant kq.
Measuring fluorescence
The configuration of a fluorescence spectrometer is shown below:
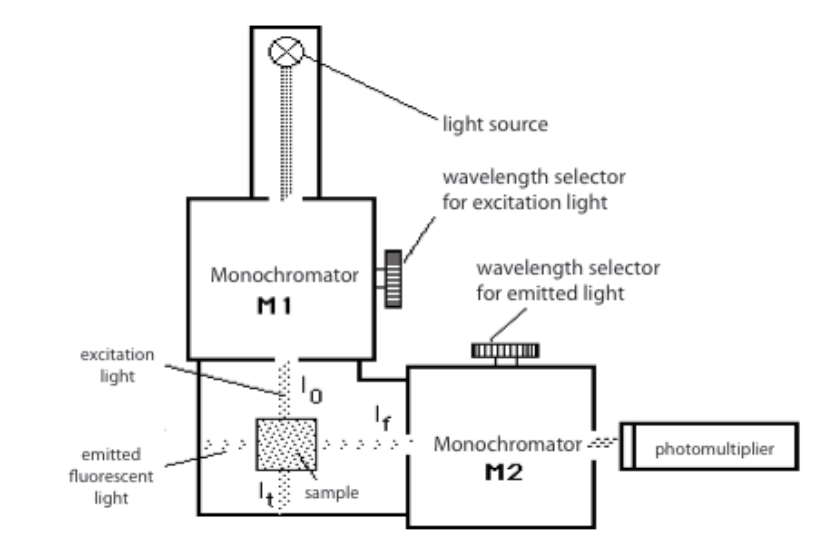
The main components of a fluorescence spectrophotometer
UV/visible light goes through monochromator M1 where the wavelength of the excitation light is chosen. While the excitation light passes the sample, the intensity of the emitted fluorescent light is measured by a photomultiplier tube set at an angle of 90° to the excitation beam. The fluorescent light passes through monochromator M2 allowing only light with a chosen wavelength to pass.
The intensity of the fluorescent radiation If is a function of both the excitation wavelength and the emission wavelength. Two types of spectra are distinguished:
a) Excitation spectra:If is measured as a function of the excitation wavelength, while the emission wavelength is kept constant.
b) Emission spectra:
If is measured as a function of the emission wavelength, while the excitation wavelength is kept constant.
The figure below illustrates how the fluorescence of anthracene varies as a function of the excitation and emission wavelengths.
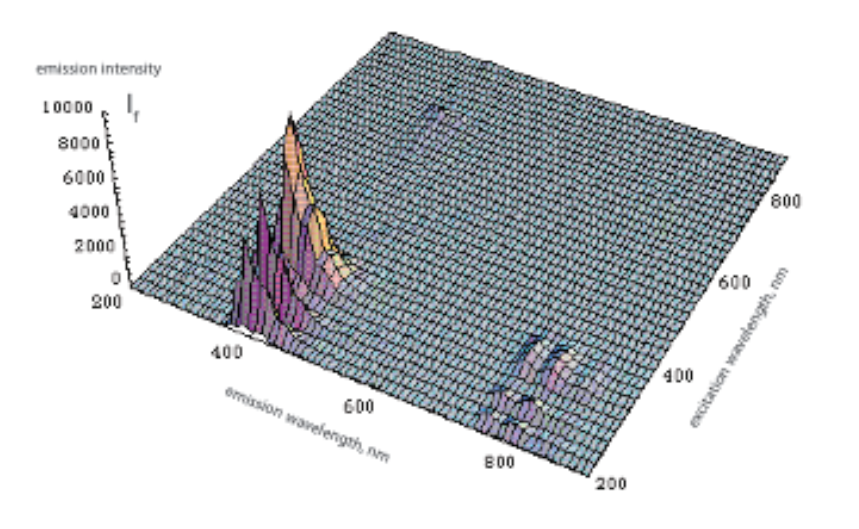
3D-fluorescence spectrum of anthracene in n-hexane
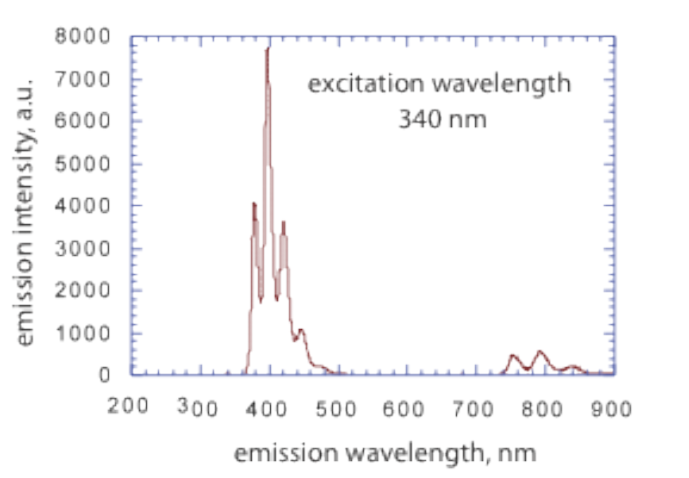
Emission spectrum of anthracene in n-hexane
In this experiment we will measure the emission intensity of anthracene at 398 nm when the molecule is excited at 340 nm.
Practical guidance of the experiment
A stock solution of 1.0 × 10-4 M anthracene in n-hexane and a 1.5 × 10-2 M solution of CBr4 where the anthracene solution is used as solvent is available.
Make 10 mL samples solutions containing 0%, 4%, 16%, 28%, 40%, 52%, 64%, 76%, 88%, and 100% of CBr4 (all by vol%) of the 1.5 × 10-2 M solution of CBr4 described above. Use the anthracene stock solution for dilution. Measure the fluorescence intensities for all solutions at λex= 340 nm and λem = 398 nm. See the dataset below
Let I0 denote the fluorescence intensity of anthracen when CBr4 is absent (no quencher), and let I denote the intensity when the quencher (CBr4) varies.
Calculate (I0 / I) -1 for the different CBr4 concentrations and plot (I0 / I) -1 versus [CBr4] (Stern-Volmer plot). Draw a linear regression line through the data points by the use of Excel. Determine the slope and calculate the rate constant kq based on the fact that the relaxation time of the photoexcited condition of A* for anthracen is τ = 5.52 × 10-9 s (we can assume temperature independence).
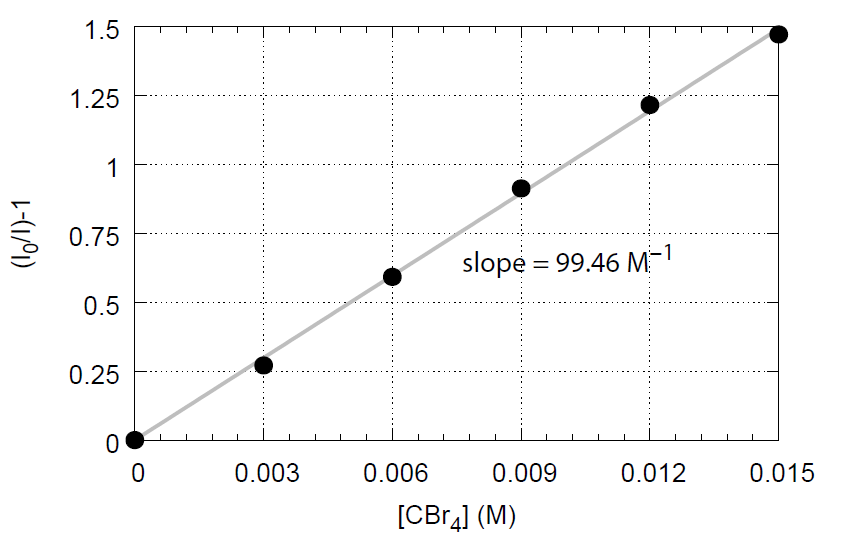
Stern-Volmer plot of fluorescence quenching of anthracen with CBr4
Also estimate kq at 20 °C according to equation 22. The viscosity of n-hexane as a function of temperature is given in this table:
| Temperature, °C | Viscosity of n-hexane, cP |
|---|---|
| 17 | 0.374 |
| 20 | 0.326 |
| 25 | 0.294 |